Merge Sort in Python

Merge sort is a fast sorting algorithm that works by dividing the array into smaller subarrays and then sorting each subarray individually. After that, the subarrays are combined to form the complete sorted array. It is a recursive procedure so it requires additional space. However, its run time is O (n log n).

Dry Run

The initial array of size n is divided into two arrays of size (n/2). Then these arrays are divided into 4 arrays of size (n/4). This process repeats until we have n arrays of size 1. After that, we start combining these arrays by putting the elements in the sorted order to finally form the sorted array.

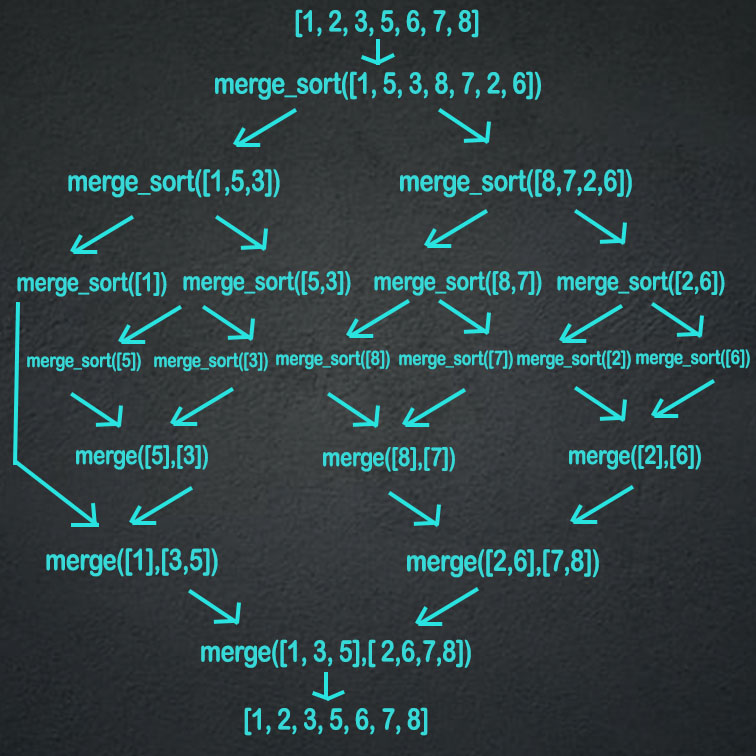
Implementation

The merge procedure takes two arrays and puts its elements into a new array in the sorted form. The merge sort is a recursive procedure that divides the array into half at each step and calls the merge procedure on the two halves and then finally returns the merged array. 

def merge(arr1,arr2):
    m=len(arr1)
    n=len(arr2)
    newarr=[]
    i=0
    j=0

    while i<m and j<n:
        if arr1[i]<=arr2[j]:
            newarr.append(arr1[i])
            i+=1
        else:
            newarr.append(arr2[j])
            j+=1

    while i<m:
        newarr.append(arr1[i])
        i+=1

    while j<n:
        newarr.append(arr2[j])
        j+=1

    return newarr
        
def merge_sort(arr):
    if len(arr)==1:
        return arr

    middle=len(arr)//2
    left=merge_sort(arr[0:middle])
    right=merge_sort(arr[middle:])

    merged_arr=merge(left,right)

    return merged_arr
        
arr=[1, 5, 3, 8, 7, 2, 6]
print("Initial unsorted list = ",arr)

sorted_arr=merge_sort(arr)

print("Final sorted list = ",sorted_arr)
Output
Initial unsorted list =  [1, 5, 3, 8, 7, 2, 6]
Final sorted list =  [1, 2, 3, 5, 6, 7, 8]

Time Complexity Analysis

Merge sort has the same best case, average case, and worst case complexity i.e O(n logn).
Explanation : At every step, the array is divided into half. So, it would take log n steps to break the array into multiple arrays of size 1. After that, we combine these arrays two at a time by comparing the elements of both arrays and putting them in sorted order. In this way, we get (n/2) arrays of size 2. We again repeat the same for these arrays to get (n/4) arrays of size 4 and so on until the final array is obtained. This would take O(n) time at each step for combining the intermediate arrays. At every step, there are n comparisons. Hence, the total complexity is O(n logn).

Advantages and Disadvantages

Advantages :
  1. It takes O(n log n) time to sort the array in all the cases i.e best case, average case and worst case. Therefore, it is efficient for sorting a large amount of data.
  2. It is a stable algorithm i.e relative order of the same elements is preserved.
Disadvantages :
  1. Requires additional space.